Sometimes a superficially small tweak to a task - changing just one little thing - can dramatically alter it, and mean that a lot more thinking - or very different thinking - is needed. In many cases, students don't need to be taught any additional facts or methods beyond what they have already learned - they know everything necessary to be able to figure out what difference the change makes.
The details matter in mathematics task design and adaptation. Here are just a few examples of small ways in which tasks can be adapted to make them more challenging and so that they may provoke deeper thought. For more on ways to adapt mathematics tasks, see Prestage and Perks (2013). The tasks below all take the form "You know this, but what about this?"
1. Change the base
It's sometimes said that You don't understand long division until you can do it in any base.
You know how to work out $252 \div 6$ in base $10$, but can you do it in base $16$?
In which other bases does $252 \div 6$ give an integer answer? Why?
Doing arithmetic in different bases used to be much more common in UK mathematics teaching, and it is still quite prevalent in schools in many countries. I find that people often assume that it's much more complicated than it is. I once heard a staffroom conversation that went something like this:
A: I think we're just too obsessed with base 10 and we don't take opportunities to work in other bases.
B: Yes, I guess it's just a convenience thing - it's so handy, for example, to be able to multiply by 10 by just placing a zero on the end.
A: Do you know how to multiply by 7 in base 7?
B: Er, no, not off the top of my head, but I should think it's very complicated. That's my point about why we always resort to base 10.
Exploring factors of numbers in different bases can be a good way to see why person B is wrong about this!
You know the factors of $12$ in base $10$, but what are the factors of $12$ in base $16$?
In which bases is $12$ prime? Why?
By changing something, away from the familiarity of base 10, we can 'make the familiar strange' and see things in new ways. It is such an apparently small change, but there are many tasks in which a change of base can be insightful (see Foster, 2007). For example,
You know that, in base 10, $\frac{1}{2}$ is a terminating decimal and $\frac{1}{3}$ is a recurring decimal. Which fractions terminate and recur in other bases? Is there a base in which $\frac{1}{2}$ is a recurring decimal and $\frac{1}{3}$ is a terminating decimal? Or in which they are both recurring or both terminating? What is $\frac{1}{2}$ in base 16? What about in base 15? What about in other bases?
2. Introduce modulus signs
The definition of the modulus function is very simple. You could use the ideas below when teaching students about the modulus function for the first time. But you could also use them with any students - even quite young ones - who don’t ‘need’ to learn about the modulus function. You would be using the modulus function as a way to get them to think more deeply about things they do 'need' to think about.
The modulus function $\lvert x \rvert$ is defined as:
$$\lvert x \rvert=\left\{ \begin{array}{@{}ll@{}} x, & \text{if}\ x \ge 0 \\ -x, & \text{if}\ x \lt 0 \\ \end{array}\right.$$
But the idea is much simpler and more accessible than this formal notation might suggest. The value of $\lvert x \rvert$ is the absolute 'size' of $x$, regardless of its sign. So $\lvert 18 \rvert = 18$, but $\lvert -18 \rvert = 18$ also. This means that $\lvert x \rvert$ is never negative (Note 1).
That is all the formal teaching that is needed. The task is then is to try some things that students can already do, but with a modulus function thrown into the mix - a superficially small change, but with a 'butterfly' effect.
You know what the graph of $y=\sin x$ looks like. What about $y=\lvert \sin x\rvert $? Or $y=\sin \lvert x \rvert$?
You know what the graph of $y=x+1$ looks like. What about $y=\lvert x \rvert+1$ or $y=\lvert x+1 \rvert$?
You know what the graph of $y=(x+1)^2$ looks like. What about $y=\lvert x+1 \rvert^2$? Or $y=( \lvert x \rvert + 1)^2$?
You know how to solve $3x-2=10$. What about $\lvert 3x-2 \rvert =10$?
You know how to solve $3x-2=2x+1$. What about $\lvert 3x-2 \rvert = \lvert 2x-1 \rvert$?
You know how to solve $3x-2<2x+1$. What about $\lvert 3x-2 \rvert < \lvert 2x-1 \rvert$?
You know how to find the integral $\int (x^2-1) dx$. What about $\int \lvert x^2-1 \rvert dx$?
Introducing modulus signs is a little like introducing $\pm$ signs (see Foster, 2012) in that you are making a superficially small change that has the effect of requiring students to think quite hard.
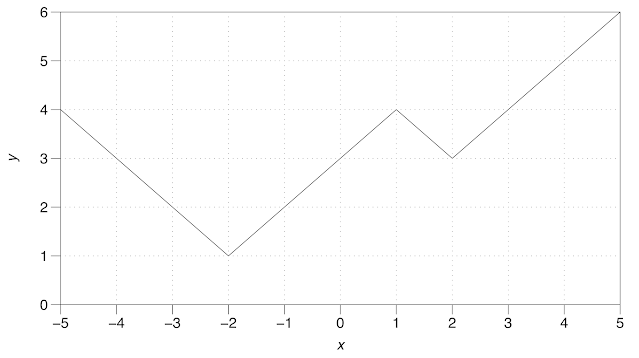
Finally, for modulus functions, take a look at this graph:
What combination of modulus functions could produce this graph? (See Note 2 for the answer.)
3. Go non-linear
Older students may know, or have a sense of, what happens if you change a function $f(x)$ into, say, $f(-x)$, or $f(mx)$, where $m$ is a constant. But what happens to well known graphs of $y=f(x)$ if we change:
- $x \mapsto \frac{1}{x}$; e.g., $\sin {(\frac{1}{x})}$, $e^{\frac{1}{x}}$?
- $x \mapsto x^2$; e.g., $\sin {x^2}$, $e^{x^2}$?
4. Look for in-between values and concepts
You probably know what the graph of $y=x^n$ looks like for positive integer $n$ and for $n=-1$. But what about for other negative integer $n$? And what about for non-integer $n$, both positive and negative (Note 2)?
You probably know about 'highest common factors' (or 'greatest common divisors'). What about 'second-highest common factors'? When do/don't they exist? What can you work out about them?
You probably know about 'common multiples' as the numbers where sequences like $3n$ and $8n$ intersect. But where do sequences like $3n+1$ and $8n-2$ intersect?
You probably know how to construct a perpendicular bisector? How would you construct a perpendicular trisector?
Conclusion
Variation theory currently receives a lot of attention, and can be powerful for helping students attend to what is the same and what is different in a sequence of tasks. In this spirit, little changes beyond what students need to know, and into unknown terrain, can be interesting extension tasks and valuable tasks for everyone to deepen their knowledge and understanding.
Questions to reflect on
1. What other butterfly examples do you have, where 'changing one little thing' has a big effect?
2. When would you use tasks like this?
Notes
1. Of course, the notation $\lvert x \rvert$ is also used where $x$ (perhaps written as $\textbf{x}$) is a vector, or where $x$ is a complex number, or to indicate the determinant of a matrix (in which case $\lvert x \rvert$ could be negative). But in this post I am only thinking about $x$ as a real number ($x \in \mathbb{R}$).
2. The graph is $y= \lvert x-2 \rvert + \lvert x+2 \rvert - \lvert x-1 \rvert$. Students could invent tasks like this for each other.
3. If you use software to draw $y = x^n$, and set up a slider to vary the value of $n$, you may notice a 'flickering' behaviour for negative values of $x$. It is interesting to think about why this happens. If $n$ is rational and equal to $\frac{p}{q}$, where $p$ and $q$ are integers, $q \neq 0$, and $\frac{p}{q}$ is in its lowest terms, then the domain of $x$ is:
- all of the real numbers, if $q$ is odd, but
- all of the non-negative real numbers, if $q$ is even.
This means that, when $n$ is real, but not rational, the domain is all the non-negative real numbers. So, the graph flickers as you drag the slider because, as $n$ varies, the function keeps switching between being defined and undefined (see also Dobbs, 2017).
References
Dobbs, D. E. (2017). Why the $n$th-root function is not a rational function. International Journal of Mathematical Education in Science and Technology, 48(7), 1120-1132. https://doi.org/10.1080/0020739X.2017.1319980 ($\$$)
Foster, C. (2007). Twenty–one forever! Journal of Recreational Mathematics, 36(3), 194–195. https://www.foster77.co.uk/Foster,%20Journal%20of%20Recreational%20Mathematics,%20Twenty-One%20Forever.pdf
Foster, C. (2012). Plus–minus graphs. Mathematics in School, 41(2), 32–33. https://www.foster77.co.uk/Foster,%20Mathematics%20in%20School,%20Plus-Minus%20Graphs.pdf
Prestage, S., & Perks, P. (2013). Adapting and extending secondary mathematics activities: New tasks for old. David Fulton Publishers.