Does anyone teach lines of best fit 'properly' in lower secondary school? I think whenever I’ve seen this concept taught, or taught it myself, it’s always been a bit wrong.
Typically, students are given a scatterplot, or they draw one themselves, and are asked to draw a straight line on top of it, by eye, but the instructions for how they are supposed to draw this line can be a bit vague. Maybe the teacher says something like, “The 'line of best fit' goes roughly through the middle of all the scatter points on a graph.” (BBC Bitesize: https://www.bbc.co.uk/bitesize/guides/zrg4jxs/revision/9) I guess this is kind of right, but I think that any student hearing this is bound to misinterpret what this is supposed to mean.
Suppose you give students the $x$-$y$ scatterplot below (Note 1), and ask them to draw the best straight line they can that takes account of all these points.
Of course, they could draw something like this, which “goes roughly through the middle of all the scatter points” (10 points on either side).
But, unless they are trying to be awkward, they will probably be much more likely to draw something like this.
It 'goes through the middle' and is the kind of thing that the teacher is wanting (Note 2).
But, if you then display an accurate trend line, say using Excel (in black below), then it will be a bit off from what the students have drawn.
Here they are together, so you can see the difference:
It is easy to put this discrepancy down to human error. The computer draws the best possible line, and the line we draw by eye is bound to be not quite right. Students might over-attend to a few prominent outliers, rather than really base their line on where the overall mass of the points is located. So there is nothing to worry about.
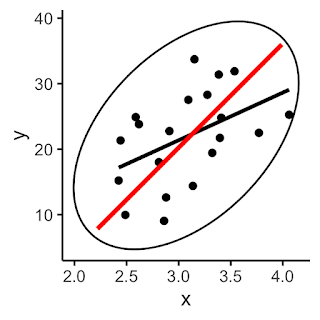
But there is more than random error going on here. I claim that the students are not even trying to draw the line that the computer is drawing. For example, if we switch the variables around (interchange the axes), presumably this would/should make no difference at all to the line that the students are trying to draw, relative to the positions of the points – it should just be a reflection of their line in the diagonal $y=x$. But the computer will give you a completely different regression line, because the regression line of $y$ on $x$ is in general quite different from the regression line of $x$ on $y$ - and sometimes dramatically so. The regression line of $x$ on $y$ is shown in blue below, on top of the black regression line of $y$ on $x$.
The black line minimises the sum of the squares of the vertical distances of the points from the line, whereas the blue line minimises sum of the squares of the horizontal distances of the points from the line. We should not expect the resulting lines to be the same. The black line gives the best linear prediction of the $y$ value, given the $x$ value; the blue line gives the best linear prediction of the $x$ value, given the $y$ value. The two lines answer two different questions.And neither of these questions is likely to be what the students are thinking about. The line the students are likely to be aiming for is the principal axis of the data. If we draw an ellipse around our data points, what the students are presumably trying to do is essentially find the major axis of this ellipse.
If we compare the principal axis (in red below) with the correct regression line of $y$ on $x$ (in black), we can see that they are not the same.
If you consider thin, vertical slices of the ellipse, the black line approximately bisects these, and is close to the mean $y$-value of the points that are near to that value of $x$. Relative to this, the red line underestimates $y$ for low values of $x$ and overestimates them for high values of $x$.In school mathematics, lines of best fit are used to predict one variable from the other, so it's really regression lines that we need, not principal axes. (And, indeed, really we should use a different line to predict $y$ from $x$ [part (b) of the typical exam question, in which part (a) is to draw the line of best fit] from the line we use to predict $x$ from $y$ [part (c) of the typical exam question].) Even when the regression line and the principal axis happen to be close to each other, conceptually they are quite different. The principal axis minimises the sum of the squares of the (perpendicular) distances from the points to the line, whereas the ordinary-least-squares regression line minimises the sum of the squared vertical distances from the points to the line. It can be interesting to devise scenarios where these two lines are very similar and very different.
From a school teaching point of view, does this matter, or is it unnecessary quibbling? I have found that this discussion comes up sometimes when students complain that the line of best fit that the computer is producing ‘looks wrong’, especially when there are lots of points, and the correlation is fairly strong. They think they can draw a better one, and are puzzled why the computer is clearly giving them 'wrong' lines. The problem here is that the students have been misled about which line they should be aiming for, and Gelman and Nolan (2017, Chapter 4) have a nice approach to addressing this.
Maybe it is a relatively small point to worry about, but surely it would be a bit of a problem if students drawing something closer to the black line above were being penalised or criticised over those drawing something more like the red line.
Questions to reflect on
1. How concerned are you about this distinction between regression lines and principal axes?
2. What, realistically, might be done to address this in school-level mathematics?
3. Are there other examples in school mathematics where it is usual to teach things 'a bit wrong'?
Notes
1. The data used in this blogpost is available at: https://www.foster77.co.uk/Data%20for%20line%20of%20best%20fit%20blogpost.csv
2. Students sometimes have a strong tendency to avoid going directly through any of the points. They have been told that they are not meant to 'join up' the points, and, as if to prove this, they try to keep away from any actual points altogether. Similarly, they may feel that it would be wrong to allow the line to pass directly through the origin, so they act as though the origin must be avoided at all costs.
Reference
Gelman, A., & Nolan, D. (2017). Teaching statistics: A bag of tricks. Oxford University Press.












Another fascinating post. To me this shows that calculated lines of best fit are several bridges too far for GCSE. Everything depends on the modelling assumptions used, and not only are these quite sophisticated in themselves but the whole concept of modelling assumptions is probably too advanced for GCSE. This is a typical example of the way in which Excel makes it very easy to draw poor or confusing charts. GCSE students aren't in a position (or at least don't have time) to discuss the question, "what do you mean by a line of best fit?"
ReplyDeleteIt might have been nice to mention the fact that, in your diagram showing the ellipse and black line, the black line goes through the points where the vertical tangents to the ellipse meet the ellipse. (This of course follows from your comment about "thin vertical slices".) The line of x on y goes through the corresponding points for the horizontal tangents. But then we start having to worry about controlled variables or bivariate data.
I'd also suggest that this raises the question of whether a least-squares line of best fit is necessarily the best to use. Certainly it gives a high priority to minimising large distances of points from the line. Is this what we want? Are not the points far from the line the ones that should have less weight? Should we not want to give more emphasis to the points close to the line? Do we not just use the least-squares line because it has the simplest algebraic properties?
I think we should just suppress any idea that there is a best-fit line that can be calculated, until we have the tools to discuss the issue properly.